Mit der Effizienzmessung lässt sich beschreiben, ob eine Maßnahme geeignet ist, ein vorgegebenes Ziel in einer bestimmten Art und Weise zu erreichen.
Effizienzmessungen sind deshalb zentrale Werkzeuge für das Management. Um Effizienzmessungen richtig einsetzen zu können ist zunächst etwas Theorie notwendig.
Die Ökonomie kennt zwei Beschreibungen von Effizienz: Maximale Effizienz ist unter gegebenen Umständen erreicht, wenn bei vorgegebenem Mitteleinsatz ein möglichst hoher Ertrag erreicht wird (Maximalprinzip) oder wenn man ein vorgegebenes Ziel mit dem geringsten Mitteleinsatz erreicht (Minimalprinzip).
Damit ist die Effizienz ein Maß für die Wirtschaftlichkeit und so ein zentrales Kriterium für rationale Managemententscheidungen.
Davon zu unterscheiden ist die Effektivität. Effektivität ist ein Maß für Wirksamkeit, ausgedrückt als Verhältnis von erreichtem Ziel zu definiertem Ziel. Dies ist im Unterschied zur Effizienz (als Maß für Wirtschaftlichkeit) unabhängig vom Aufwand. Einzig, inwieweit das definierte Ziel unter Ausmaß und Qualität erreicht wird, stellen die Kriterien für Effektivität dar.
Wir halten es für die Unterscheidung von Effizienz und Effektivität mit Peter F. Drucker
“It is fundamentally the confusion between effectiveness and efficiency that stands between doing the right things and doing things right. There is surely nothing quite so useless as doing with great efficiency what should not be done at all.”
Deutsch frei übersetzt: Effektivität: „Die richtigen Dinge tun.“ Effizienz: „Die Dinge richtig tun.“
Wir haben zur Effizienzmessung ein lesenswertes working paper der Universität Lüneburg von Anne-Kathrin Last und Heike Wetzel für Sie gelesen. Dieses work paper verwenden wir auch für die folgenden Ausführungen.
Quellenangabe: Teile der folgenden Ausführungen zu Effektivität, Effizienz, vor allem aus Sicht des Vertriebs sind dem Buch: Tobias Englet, Steuerung der Effizienz und Effektivität im Vertrieb zur Unternehmenswertsteigerung, Hamburg 2012, ISBN: 9783656656128 entlehnt. Download dieses Artikels
Sowohl aus betriebswirtschaftlicher als auch aus volkswirtschaftlicher Sicht ist es von zentraler Bedeutung, wie effizient während eines Produktionsprozesses Inputs in Outputs umgewandelt werden. Aus betriebswirtschaftlicher Sicht ist die Effizienzmessung besonders im Hinblick auf das Benchmarking intern als auch gegenüber Konkurrenten wichtig. Firmen können so ihren eigenen Produktionsprozess mit Best-Practice-Unternehmen in ihrer Branche vergleichen, Verbesserungspotenziale erkennen und effizienzsteigernde Strategien entwickeln.
Trotz ihrer großen Bedeutung in der wirtschaftlichen Forschung und Praxis besteht zum einen noch kein Konsens, was beide Begriffe genau ausdrücken, zum anderen – was sich noch schwerer gestaltet – wie die Begriffe voneinander abgegrenzt werden können. Folgendes Zitat will das Begriffswirrwarr beider Ausdrücke zueinander auflösen:
„It is fundamentally the confusion between effectiveness and efficiency that stands between doing the right things and doing things right.”
Effektivität steht dafür, aus einer Anzahl von möglichen Handlungsalternativen „die richtigen Dinge zu tun“.
Somit bezeichnet Effektivität im weiteren Sinne (i.w.S.) die „Wirksamkeit” einer Maßnahme auf ein Ziel, also: „Werden vorgegebene Ziele erreicht?“
Um messen zu können, ob Ziele erreicht wurden, ist der Output und damit der Nutzen der getroffenen Maßnahme entscheidend. Deshalb wird Effektivität auch gleichgesetzt mit der absoluten Höhe des „Outputs der Leistungserstellung“.
Effektivität im engeren Sinne (i.e.S.) steht für den Zielerreichungsgrad, d.h. die Wirksamkeit einer Maßnahme wird hier ins Verhältnis zu einem vorab definierten Zielniveau gesetzt. Relevant ist demnach das Verhältnis von momentanem Output zum festgelegten Ziel. Unternehmen managen diese Art der Effektivität mit Soll-Ist-Vergleichen.
Die Vielfalt von unterschiedlichen Definitionen des Begriffs Effizienz verdichtet sich in folgenden Schwerpunkten:
Effizienz als
- Verfolgung des ökonomische Prinzips,
- Identifizierung von Handlungsalternativen,
- Verbesserung des Grads) der Zielerreichung,
- Realisierung einer günstigen Input-/Output-Relation,
- Forderung „to do things right”.
Die häufigste Definition der Effizienz im Management ist die Verfolgung des ökonomischen Prinzips in der klassischen Ausprägung, ein vorgegebenes Ziel mit geringstem Mitteleinsatz zu erreichen. Dazu wird der Mitteleinsatz bestimmt und minimiert. Meist wird in Geldeinheiten gemessen. Es sind aber z.B. bei Umweltzielen auch andere physikalische bzw. chemische Größen als Messeinheit üblich. Bei Vergleichen muss nur über gleiche Messeinheiten sichergestellt werden, dass man nicht "Äpfel mit Birnen" vergleicht. Misst und vergleicht man in Geldeinheiten, wird "Geld" als Verrechnungseinheit genutzt.
Bei minimalen Ressourceneinsatz steigt die „Input/Output-Relation“als Maß für die Effizienz. Im Gegensatz zur Effektivität setzt die Effizienz die Höhe des Outputs ins Verhältnis zum eingesetzten Input.
Hier wird dabei aber der enge Zusammenhang zwischen Effektivität und der Effizienzmessung in der Praxis deutlich:
Das Management wählt in der Entscheidungsfindung in einem ersten Schritt aus mehreren Handlungsalternativen nach dem Effektivitätskriterium die Alternative mit dem höchsten „Zielnutzen“ aus. Erst im zweiten Schritt wird unter Effizienzkriterien untersucht, auf welche Art und Weise die gewählte Handlungsalternative mit höchstem Output bzw. minimalem Mitteleinsatz erreicht wird. Effektivität beschreibt also das Ziel und Effizienz den optimalsten „Weg“, der zu diesem Ziel beschritten werden muss.
Wichtig ist also bei der Auswahl geeigneter Managementwerkzeuge im Controlling die Untersuchungsabfolge auch einzuhalten: Effektivität i.w.S. ist die notwendige Voraussetzung für eine Effizienzmessung. Erst mit Festlegung eines Ziel, gemessen mit einem geeigneten Effektivitätsmaß kann das Effizienzkriterium angewendet werden. Das wird in der Praxis oft vernachlässigt, bzw. noch schlimmer, das Management legt sich hier nicht fest und "stochert" dann eigentlich "im Nebel herum".
Budgetierung:
Zumindest bei großen Unternehmen bzw. Unternehmen mit einer klaren Budgetierung auf Jahresbasis oder anderer gewählter Budgetierungszeiträume steht die zweite Ausprägung des ökonomischen Prinzips im Vordergrund, ein maximales Ergebnis bei vorgegebenem (eben budgetiertem) Input/Mitteleinsatz zu erzielen.
In vielen Unternehmensbereichen (z.B. beim Vertrieb und auch bei Marketing und Werbung ist diese Vorgehensweise in der Praxis i.d.R. zu finden.
Oft können entscheidende Inputfaktoren, z.B. die Anzahl von Filialen oder Niederlassungen nur begrenzt variiert werden. Eine Optimierung der Inputfaktoren ist also oft gar nicht in der gebotenen Anpassgeschwindigkeit möglich. Daher wird hier richtigerweise eine effizientere Transformation eines gegebenen Inputniveaus in einen höheren Output gefordert.
Fazit: Da bei beiden Sichtweisen die minimalen Input- und maximalen Outputmengen häufig unbekannt sind, wird die bestmögliche Relation durch einen Vergleich meist vieler (Faktor)-Kombinationen von Input und Output zu ermitteln sein. Das sind recht komplexe Managementaufgaben, die nur durch mehrdimensionale Instrumente unterstützt werden können. Vorsicht also bei Scheinlösungen mit Standardanwendungen. Eine sorgfältige Vorabanalyse der konkreten Ist-Situation ist Voraussetzung, um dann eine klare und transparente Entscheidung mit sorgfältig festgelegten Auswahlkriterien treffen zu können, um hier konkurrenzfähig zu sein und zu bleiben.
Um komplexere Entscheidungsalternativen vergleichen zu können hat die Ökonomie das Kriterium der Pareto-Effizienz entwickelt. Pareto- effizient sind dabei solche Zustände bzw. Faktorkombinationen, die nicht mehr verbessert werden können ohne sich an anderer Stelle eine Verschlechterung einzuhandeln; d h., solange es möglich ist Verbesserungen zu erzielen, ohne das sich andere Kriterien bzw. Faktoren verschlechtern, ist Pareto-Effizient noch nicht erreicht und das Verbesserungspotenzial ist noch eindeutig.
Ein Beispiel:
Man kann z.B. den Vertrieb eines Unternehmens für sich allein genommen optimieren, also effizient gestalten. Pareto-Optimalität ist dann erreicht, wenn man den Vertrieb nicht mehr effizienter machen kann, ohne dass z.B. die Kundenzufriedenheit sinkt und dann Umsatzeinbrüche die Folge sind.
In unseren Balanced Scorecard Systemen sind derart komplexen Zusammenhänge relativ leicht einzubauen bzw. dann auch zu managen. Es muss dabei komplex "gemessen" werden, um richtig managen zu können.
Oft ist dabei aber die unternehmensinterne Auseinandersetzung zwischen Vertriebschef oder -cheffin und Marketingchef oder -cheffin deutlich informativer und zielführender als falsche oder mangelhafte Kennzahlen. Gute Scorecardsysteme können das klar abbilden und auch zu rationalen Entscheidungen führen.
Werden Effizienz und Effektivität in Zusammenhang mit dem Fachbereich des Vertriebs gebracht, gelangen wir zur Vertriebseffizienz und -effektivität (VEE). Die Untersuchungseinheiten für das Effizienz- wie auch für das Effektivitätskriterium sind hier Organisationseinheiten des Vertriebs, wie Vertriebsmitarbeiter, Händler oder das ganze Vertriebssystem. Diese handeln bei der Entscheidungsfindung effektiv, wenn sie die Handlungsalternative mit dem größten Nutzen zur Erreichung eines Vertriebsziels – meist ausgedrückt durch eine Kennzahl – wählen. Effizient sind die Vertriebseinheiten, wenn sie „ihre Ressourcen zur Akquisition neuer Kunden, deren Bindung und Cross-Selling so einsetzen, dass sie ihr spezifisches Marktpotential ausnutzen“ und die dafür benötigten Aktivitäten des Warentransports und -bereitstellung möglichst kosten- und zeitminimal ausführen.
Es ist möglich, Effizienz und Effektivität im Fachgebiet des Marketing zusammenzufassen, indem auf Basis der bisherigen Grundlagen aus beiden Begriffen das zweidimensionale Konzept der Marketing Performance entsteht. Effizientes Handeln stellt sicher, dass das Unternehmen kurzfristig auf Erfolgskurs bleibt und ist daher eher operativer Natur. Dagegen ist die Effektivität ein strategisches Konzept, in dem Aufgaben wie die Unternehmensstrategie oder die Positionierung von Produkten ausgearbeitet werden. Es ist einleuchtend, dass effektive Handlungen nicht unbedingt effizient sein müssen, beispielweise wenn Ziele ohne jegliche Kostenkalkulation verfolgt werden. Umgekehrt führt beispielsweise eine effiziente Planung der Vertriebskanäle, die nicht zur Unternehmensstrategie passt, zu einem niedrigen Zielerreichungsgrad und ist daher überhaupt nicht effektiv.
In der Marketing Performance werden also die Ziele der strategischen sowie operativen Marketingplanung vereint. Das Konzept ermöglicht eine Bewertung von Entscheidungseinheiten, seien sie „qualitative wie quantitative, strategische wie taktische, output- wie inputorientierte“ Faktoren.
Im Idealfall arbeitet das Unternehmen im Feld des „Performanten Marketing“, in dem im Bezug auf den Output (hier eine hohe Kundenorientierung) das Effektivitätskriterium voll erfüllt ist und gleichzeitig durch niedrige Marketingkosten „im Sinne einer günstigen Output-Input-Relation“ auch eine hohe Effizienz gewährleistet ist. Nicht viele Unternehmen können bei hoher Kundenorientierung auch die hierfür benötigten Marketingkosten auf einem niedrigen Niveau halten. Ein effektives Marketing mit geringer Effizienz zeichnet sich zwar durch zufriedene Kunden aus, die aber aufgrund ihrer Preisorientierung zu Anbietern mit einer günstigeren Kostenstruktur abwandern werden. Ein hocheffizientes Marketing mit niedriger Effektivität wird hingegen kurzfristig Gewinne vorweisen können, jedoch langfristig ohne jegliche Kundenorientierung keinen Bestand haben. Zuletzt das Feld des „Todeswunsch- Marketing“, in dem Unternehmen durch eine geringe Effektivität bei niedriger Effizienz auf dem Markt keinerlei Erfolgsperspektiven haben.
Marketing Performance bedeutet also, die richtigen Dinge (wie das Marketingziel einer hohen Kundenzufriedenheit) richtig (also wirtschaftlich) zu tun.Die Marketing Performance leistet somit einen wichtigen Beitrag zur Aufgabe des (Marketing-)Controllings, nämlich der Sicherstellung der Effektivität und Effizienz.
Diese Aufgabe der Steigerung der Effektivität und Effizienz dient seinerseits der obersten gesamtunternehmerischen Zielgröße,der Steigerung des Unternehmenswerts. Da der Vertrieb ein Teil des Marketing ist, wird auch in der vorliegenden Arbeit Effektivität und Effizienz im Vertrieb an der Zielgröße des Unternehmenswerts ausgerichtet:
Effizienz und Produktivität:
Quellenangabe: Nachfolgende Ausführungen zur Effizienz und zum Begriff der Produktivität sind der Veröffentlichung: Anne-Kathrin Last und Heike Wetzel, Effizienzmessverfahren – Eine Einführung, University of Lüneburg, Working Paper Series in Economics No. 145, 2009, www.leuphana.de/vwl/papers,ISSN 1860 - 5508, entlehnt.
Im ökonomischen Sinne bezeichnet Produktivität das Verhältnis zwischen einer produzierten Menge an Gütern (Outputs) und der dafür benötigten Menge an Produktionsfaktoren (Inputs). Sie lässt sich im Fall der Produktion eines Outputs mit nur einem Input als Quotient der beiden Maßzahlen darstellen. Werden hingegen mehrere Inputs und/oder Outputs im Produktionsprozess
berücksichtigt, müssen zunächst Indizes gebildet werden, die dann in die Produktivitätsberechnung eingehen. Um die Gesamtleistung einer Firma zu evaluieren, wird die totale Faktorproduktivität (TFP) betrachtet, die alle Inputs und Outputs berücksichtigt. Im Gegensatz dazu wird von partieller Faktorproduktivität gesprochen, wenn der Einfluss nur eines Faktors auf die Produktivität untersucht wird. Der Zusammenhang zwischen Produktivität und Effizienz kann mithilfe von Produktionsfunktionen dargestellt werden. Diese geben für jede Menge an Input (x) die hiermit maximal zu produzierende Menge an Output (y) an. Der Verlauf einer Produktionsfunktion hängt dabei vom vorherrschenden Stand der Technik ab.
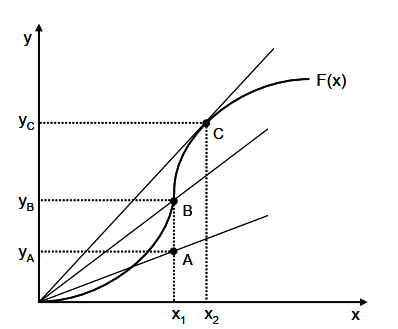
Abb. 1: Produktivität, technische Effizienz und Skaleneffizienz mit
variablen Skalenerträgen der Funktion F(x)
Beobachtete Input-Output-Kombinationen oberhalb der Funktion sind bei gegebener Technologie nicht realisierbar, weswegen die Funktion auch als Randfunktion oder Produktionsgrenze bezeichnet wird. Alle Beobachtungspunkte3 entlang der Funktion, beispielsweise B oder C, repräsentieren diejenigen Kombinationen, die technisch effizient sind: Bei gegebener Inputmenge wird die maximale Outputmenge erreicht, oder anders ausgedrückt, bei gegebener Outputmenge wird die minimal benötigte Inputmenge eingesetzt.4 Alle Input-OutputKombinationen unterhalb der Produktionsgrenze gelten als technisch ineffizient. Beispielsweise könnte ausgehend vom Punkt A der Produktionsprozess so geändert werden, dass die Outputmenge bei gleichbleibender Inputmenge x1 von yA auf yB gesteigert wird. Dies würde sowohl die Effizienz als auch die Produktivität, das heißt den Quotienten aus y und x, erhöhen.
Um die durch B und C dargestellten Input-Output-Kombinationen hinsichtlich ihrer Produktivität miteinander zu vergleichen, wird durch beide Punkte jeweils ein Ursprungsstrahl gelegt. Die Steigung jeden Strahls gibt den Quotienten aus Output- und Inputmenge und somit die Produktivität an. Es wird deutlich, dass die Produktivität in C größer ist als die in B, obwohl beide Punkte einen technisch effizienten Produktionsprozess repräsentieren. Dieser Unterschied in der Produktivität hängt von der Skaleneffizienz ab, welche wiederum von der Firmengröße bestimmt wird. Die maximale Produktivität wird in Punkt C erreicht, bei dem der Strahl aus dem Ursprung eine Tangente zur gegebenen Produktionsfunktion ist. Da alle Punkte links von C steigende und alle Punkte rechts von C fallende Skalenerträge aufweisen, wird der Punkt C als skaleneffizient bezeichnet. Im Vergleich dazu ist B skalenineffizient. Im Zeitverlauf kann ein Unternehmen somit seine Produktivität sowohl durch eine Verbesserung der technischen Effizienz als auch der Skaleneffizienz erhöhen.
Eine dritte Größe, durch die die Produktivität eines Unternehmens über die Zeit gesteigert werden kann, ist der technische Fortschritt. In Abbildung 2 resultiert dieser in der höheren Produktionsfunktion Ft+1(x), bei der für jede gegebene Inputmenge die Outputmenge höher ist als bei der Produktionsfunktion Ft(x). Beispielsweise wird durch die verbesserte Technologie im skaleneffizienten Punkt Ct+1 eine höhere Outputmenge bei niedrigerer Inputmenge im Vergleich zum Punkt Ct erreicht, was zu einer höheren Produktivität führt. Somit hängt die Entwicklung der Produktivität einer Firma über die Zeit von der Veränderung der technischen Effizienz, der Veränderung der Skaleneffizienz sowie dem technischen Fortschritt ab.
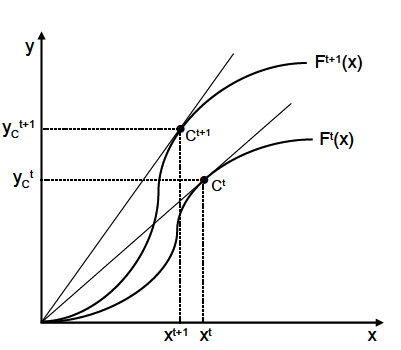
Abb.2: Produktivität mit technischem Fortschritt
Stehen zusätzlich zu physischen Input- und Outputdaten auch monetäre Daten in Form von Inputpreisen zur Verfügung, können neben der technischen Effizienz auch die allokative und die Kosteneffizienz berechnet werden. Allokative Effizienz hinsichtlich der Inputs liegt vor, wenn derjenige Inputmix gewählt wird, mit dem eine gegebene Outputmenge zu minimalen Kosten hergestellt werden kann. Sie stellt somit bei einer monetären Betrachtung der Effizienz ein weiteres Element der Produktivität beziehungsweise der Produktivitätsentwicklung über die Zeit dar. Die Kosteneffizienz ist das Produkt aus technischer und allokativer Effizienz; sie beschreibt generell die Produktion einer bestimmten Outputmenge zu minimalen Kosten unter Berücksichtigung eines effizienten Produktionsprozesses und eines effizienten Inputmixes. Allokative und Kosteneffizienz hängen beide vom gegebenen Faktorpreisverhältnis ab.
Quellenangabe: Teile der folgenden Ausführungen zu Effektivität, Effizienz, vor allem aus Sicht des Vertriebs sind dem Buch: Tobias Englet, Steuerung der Effizienz und Effektivität im Vertrieb zur Unternehmenswertsteigerung, Hamburg 2012, ISBN: 9783656656128 entlehnt. Download dieses Artikels
Effizienzmessung mit Kennzahlen:
Eine Methode, mit der die relative Effizienz beziehungsweise Produktivität von Firmen gemessen werden kann, ist der einfache Vergleich von betriebswirtschaftlichen Kennzahlen. Hierzu zählen zum Beispiel die Höhe der betrieblichen Personalaufwendungen, die produzierten Stückzahlen oder die Betriebskosten pro verkaufter Einheit. Diese Kennzahlen ermöglichen es, im Hinblick auf bestimmte Gesichtspunkte Rankings innerhalb des untersuchten Datensatzes zu erstellen. Hierbei können entweder nur Inputkennzahlen, nur Outputkennzahlen oder Verhältnisse von Input- und Outputkennzahlen berücksichtigt werden. Allerdings ist eine umfassende Effizienzanalyse nicht möglich, da sich je nach beobachtetem Kriterium die Rankings unterscheiden und zu inkonsistenten Ergebnissen hinsichtlich einer Gesamtbewertung führen können (vgl. zusammenfassend Hammerschmidt 2006, S. 105 f.). Werden auf Basis verschiedener Kennzahlen Rankings erstellt und anschließend miteinander verglichen, wird eine solche Untersuchung bei großen Datensätzen darüber hinaus schnell unübersichtlich. Weiterhin ist zu beachten, dass bei der Analyse von Input-OutputVerhältnissen jeweils nur ein Input und ein Output betrachtet werden. Demzufolge können nur Aussagen hinsichtlich partieller Faktorproduktivitäten nicht aber der TFP bei Produktionsprozessen mit multiplen In- und/oder Outputs getroffen werden.
Eine Weiterentwicklung der einfachen Kennzahlenvergleiche ist die Effizienzmessung mit preisbasierten Kennzahlen, mit der auch die TFP berechnet werden kann (z. B. Fisher- oder Törnqvist-Indizes). Bei diesen Verfahren werden die Inputs und Outputs in Marktpreisen erfasst, womit implizit eine Gewichtung vorgenommen wird, die den Einfluss der einzelnen Faktoren im Produktionsprozess widerspiegeln. Hierdurch ist es möglich, für die Inputs und Outputs jeweils Indizes zu bilden und anschließend die TFP zu berechnen. Neben der Effizienzmessung werden preisbasierte Kennzahlen auch genutzt, um Indizes für die Schätzung komplexerer Effizienzmessverfahren zu bilden.
Ein wesentlicher Nachteil der Effizienz- beziehungsweise Produktivitätsmessung anhand von preisbasierten Kennzahlen ist, dass die Veränderung der TFP nicht in einzelne Komponenten, wie zum Beispiel die technische Effizienz und den technischen Fortschritt, zerlegt werden kann.
Stehen für eine Untersuchung Längsschnittdaten zur Verfügung, gehen bei diesen Verfahren daher wichtige Informationen verloren. Insbesondere aus diesem Grund wird in der Literatur zur Effizienz- und Produktivitätsmessung auf die
im Folgenden dargestellten mathematisch komplexeren Verfahren verwiesen.
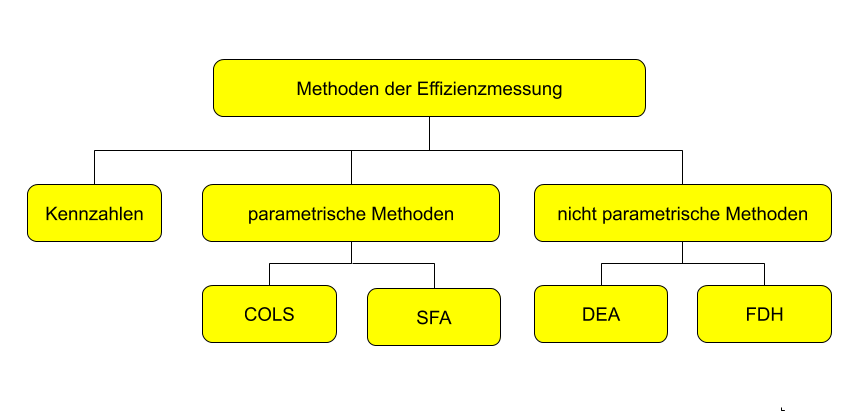
Nicht parametrische Verfahren:
Als bekannteste nicht parametrische Verfahren zur Effizienzmessung werden hier die FDH (free disposal hull) ) und die DEA (data envelope analysis) behandelt. In unseren vergleichenden Studien zur Effizienz von hotels ahebn wir die DEA erfogreich angewendet. (Link zur DEA auf dieser website).
(Vgl. auch den Beitrag DEA-der wissenschaftliche Ansatz in dieser website)
Ziel der nicht parametrischen Verfahren ist es, eine Randfunktion beziehungsweise Produktionsgrenze zu bestimmen, auf der alle technisch effizienten Beobachtungen liegen. Für alle nicht auf der Funktion liegenden Beobachtungen wird anschließend der Abstand zur Funktion gemessen, der Auskunft über die relative Ineffizienz gibt. Bei diesen Verfahren handelt es sich um lineare Programmierungsmethoden, bei denen der Verlauf der Randfunktion anhand der Beobachtungen berechnet wird.
Um das passende nicht parametrische Verfahren auszuwählen, muss a priori überprüft werden, ob für die zugrunde liegende Produktionstechnologie Konvexität angenommen werden kann oder nicht. Während das Verfahren der FDH lediglich auf der Annahme der freien Verschwendbarkeit der In- und Outputs beruht, muss für die Anwendung der DEA zusätzlich die Konvexitätsannahme erfüllt sein.Freie Verschwendbarkeit der In- und Outputs liegt vor, wenn die gleiche Outputmenge auch mit einer höheren Inputmenge als der minimal notwendigen Menge beziehungsweise wenn mit der gleichen Inputmenge auch eine geringere Outputmenge als die maximal mögliche Menge produziert werden kann. Die Konvexitätsannahme dagegen ist erfüllt, wenn jede beliebige, anteilig aus den realen Beobachtungen gebildete, Input-Output-Kombination realisierbar ist, das heißt, bei gegebener Technologie eine Produktionsmöglichkeit darstellt. Durch diese Annahme werden innerhalb der DEA neben effizienten realen Beobachtungen auch virtuelle Referenzeinheiten, bestehend aus linearen Kombinationen effizienter realer Beobachtungen, als Vergleichsmaßstab zur Effizienzmessung zugelassen.
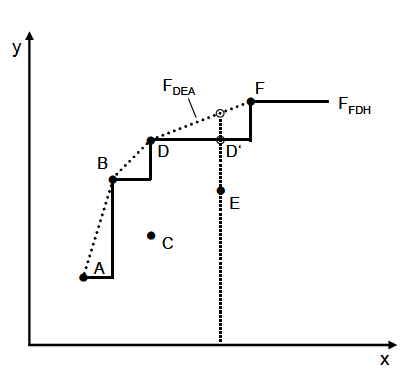
Der Verlauf mithilfe der DEA bestimmten Randfunktion hängt davon ab, ob die Skalenerträge der Produktion als konstant oder als variabel angenommen werden können. Bei konstanten Skalenerträgen führt eine Erhöhung der Inputs um einen bestimmten Faktor zu einer Erhöhung der Outputs um den gleichen Faktor, das heißt, der Funktionsverlauf ist linear. Die Lage einer solchen Funktion mit konstanten Skalenerträgen (Constant Returns to Scale, CRS) FCRS wird durch diejenige Beobachtung determiniert, deren zugehöriger Ursprungsstrahl die größte Steigung aufweist. In Abbildung 4 verläuft die Randfunktion FCRS beispielsweise durch den Punkt B, für den sich unter den gegebenen Beobachtungen die höchste Produktivität ergibt. Im Fall variabler Skalenerträge (Variable Returns to Scale, VRS) hingegen führt eine Erhöhung der Inputs um einen bestimmten Faktor je nach Skalenniveau zu einer Erhöhung der Outputs um einen niedrigeren oder einen höheren Faktor. Dies ist durch die Funktion FVRS dargestellt, die somit stückweise linear verläuft (s. Abbildung 4). Da die DEA ein deterministisches Verfahren ist, welches keine stochastischen Komponenten berücksichtigt, wird jede Abweichung einer Beobachtung zur berechneten Funktion vollständig als Ineffizienz interpretiert. Im Punkt C in Abbildung 4 wäre es beispielsweise möglich, bei gleicher eingesetzter Menge an Inputs das Outputniveau an dasjenige von Beobachtung D anzugleichen. Da diese auf der Randfunktion liegt, gilt sie als technisch effizient. Auch die Beobachtung E kann ihren Output bis zur Produktionsgrenze FVRS steigern, allerdings gibt es keine reale Beobachtung, die denselben Inputeinsatz wie E aufweist. Als Vergleichsmaßstab dient nun ein virtueller Referenzpunkt, der auf der Strecke DF liegt.
Die Abweichung der Beobachtungen zur Randfunktion FVRS gibt Aufschluss über die technische Effizienz, nicht jedoch über die Skaleneffizienz. Wenn eine Produktion mit nicht konstanten Skalenerträgen vorliegt, deren Menge an beobachteten Input-OutputKombinationen durch die Randfunktion FVRS begrenzt wird, kann die Skaleneffizienz mithilfe der Funktion FCRS bestimmt werden. Für den Punkt C entspricht die technische Ineffizienz der Strecke CD . Im Fall von konstanten Skalenerträgen könnte sogar eine Input-Output Kombination entlang von FCRS realisiert werden. Der Abstand zwischen beiden Funktionen kann somit als Skalenineffizienz interpretiert werden.
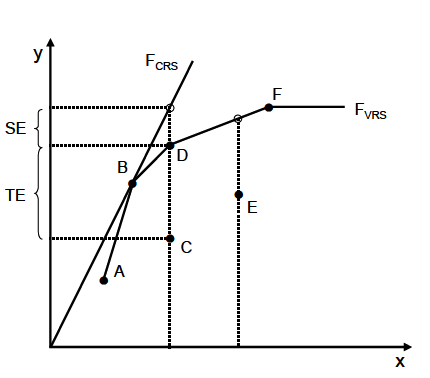
Abb.4: DEA-Produktionsfunktionen mit VRS und CRS
Ein wesentlicher Nachteil der DEA ist die auf der neoklassischen Produktionstheorie beruhenden Konvexitätsannahme, welche sowohl die beliebige Teilbarkeit der In- und Outputs als auch eine bestimmte Ausprägung der Skalenerträge in Abhängigkeit der Firmengröße impliziert. Dies hat zur Folge, dass die Modellierung einer Vielzahl theoretisch denkbarer Produktionstechnologien, zum Beispiel eine Technologie mit stetig steigenden Skalenerträgen, von vornherein ausgeschlossen ist. In diesem Fall kann zur Bestimmung der Effizienz die weniger restriktive FDH-Methode verwandt werden.
Bei diesem Verfahren sind als Referenzeinheiten auf der Randfunktion ausschließlich real
beobachtete Input-Output-Kombinationen zulässig; es werden keine virtuellen Referenzeinheiten gebildet. Als Eckpunkte für die Berechnung der FDH Funktion werden alle Beobachtungen berücksichtigt, die bei gegebenen Inputs den höchsten Output realisieren und gleichzeitig bei gegebenem Output am wenigsten Inputs einsetzen. Daher ist, wie in Abbildung 5 dargestellt, der Verlauf einer FDH-Randfunktion stufenförmig. Im Vergleich zur DEA wird nun die Ineffizienz der Beobachtung E nicht mehr mithilfe einer virtuellen Referenzeinheit auf der Strecke DF bestimmt, sondern bei einer outputorientierten Sichtweise mithilfe der Beobachtung D. Bei gleicher eingesetzter Menge an Inputs könnte die Beobachtung E ihren Output auf das Niveau der Beobachtung D steigern. Die mögliche Outputsteigerung entspricht der Strecke ED'. Hier wird ein erstes Problem der FDH-Methode deutlich: Obwohl der Punkt D' im Vergleich zum Punkt D mehr Inputs für die Produktion des gleichen Outputs benötigt, wird er bei einer outputorientierten Sichtweise als effizient angesehen und als Vergleichsmaßstab verwendet. Bei einer inputorientierten Sichtweise dagegen würde eine Firma, die in Punkt D' produziert, als ineffizient ausgewiesen werden. Im Gegensatz zur DEA erlaubt die FDH-Methode somit eine Verwendung von Einheiten als Vergleichsmaßstab, die selbst von anderen Einheiten dominiert werden.
Ein weiterer Unterschied zur DEA ergibt sich in der Höhe der ausgewiesenen Ineffizienzbeziehungsweise Effizienzwerte. Hierbei gilt, dass für eine bestimmte Beobachtung der FDHEffizienzwert immer gleich oder höher als der entsprechende DEA-Effizienzwert ist. Insbesondere bei kleinen Beobachtungsgruppen führt der Mangel an realen Referenzeinheiten dazu, dass eine Vielzahl an Beobachtungen als vollkommen effizient ausgewiesen wird. Ein aussagefähiger Vergleich der einzelnen Beobachtungen wird dadurch nahezu unmöglich.
Abb.5: FDH- und DEA-Produktionsfunktion mit VRS
Gemeinsame Probleme beider Verfahren in ihrer klassischen Form liegen in der Nichtberücksichtigung möglicher Zufalls- und Umfeldeinflüsse, der Empfindlichkeit gegenüber extremen Beobachtungen sowie dem Fehlen von statistischen Schlussfolgerungsmöglichkeiten. Es existiert jedoch eine Vielzahl von Weiterentwicklungen beider Verfahren, die diese Mängel berücksichtigen. So können beispielsweise mithilfe von Bootstrapping-Verfahren, das heißt der wiederholten Zufallsziehung von Stichproben aus immer derselben Grundgesamtheit, statistischen Eigenschaften der Effizienzwerte ermittelt und somit Verzerrungen der Werte korrigiert, Konfidenzintervalle berechnet sowie Hypothesen getestet werden. Darüber hinaus stehen parametrische und semi-parametrische Methoden, wie die "order-m frontier", die "order-α quantile frontier" oder die stochastische DEA und die stochastische FDH, zur Verfügung, die eine Berücksichtigung von Zufalls- und Umfeldeinflüssen sowie von extremen Beobachtungen bei der Effizienzmessung ermöglichen.
Parametrische Verfahren:
Bei den parametrischen Messmethoden werden die Produktionsfunktionen nicht anhand der Beobachtungen berechnet, sondern ökonometrisch geschätzt. Daher ist es notwendig, vorab eine funktionale Form für die Funktion zu spezifizieren, wodurch implizit Annahmen über die im Produktionsprozess eingesetzte Technologie getroffen werden. Üblicherweise werden lineare Funktionen, Cobb-Douglas-, CES- oder Translog-Funktionen verwandt, um den funktionalen Zusammenhang zwischen Inputs und den daraus produzierten Outputs zu beschreiben.
Eine weit verbreitete Methode, um Produktionsfunktionen zu schätzen, ist die Kleinste Quadrate- oder OLS- (Ordinary Least Squares) Methode. Bei diesem Verfahren wird eine Produktionsfunktion geschätzt, indem die quadrierten Abweichungen der Beobachtungspunkte von der Funktion minimiert werden. Hierdurch ergibt sich eine für alle Beobachtungen durchschnittliche Produktionsfunktion, die Abweichungen sowohl nach oben als auch nach unten zulässt. In Abbildung 6 ist eine geschätzte Regressionsfunktion als FOLS dargestellt. Im Hinblick auf die realisierten Input-Output-Kombinationen gelten alle Beobachtungen entlang oder oberhalb von FOLS als effizient, für alle Punkte unterhalb der Funktion wird hingegen eine ineffiziente Produktion angenommen. Dies widerspricht jedoch der eigentlichen Interpretation der Abweichungen von der Durchschnittsfunktion (Residuen) als normalverteilte stochastische Schwankungen. Somit ist es nicht möglich, anhand von OLS- Schätzern einerseits Best-Practice-Beobachtungen durchzuführen und andererseits systematische Ineffizienzen aufzudecken.
Eine Weiterentwicklung der OLS-Regression ist das COLS-Verfahren. Dieses lässt Abweichungen von der geschätzten Funktion nur nach unten zu und stellt somit in Abgrenzung zur durchschnittlichen Produktionsfunktion eine Randproduktionsfunktion oder Produktionsgrenze dar. Korrigiert wird dabei eine mithilfe des OLS-Verfahrens geschätzte Funktion, indem sie um den höchsten positiven Residuenwert nach oben verschoben wird.
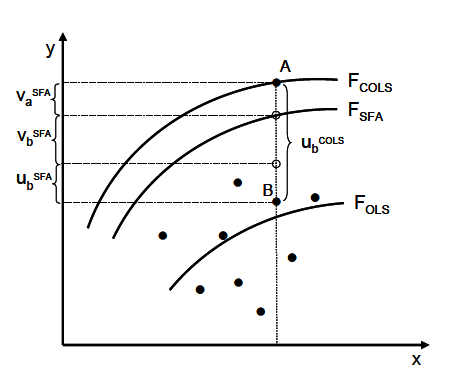
Abb.6: OLS-, COLS und SFA-Produktionsfunktionen gegenübergestellt.
In Abbildung 6 ist eine solche Funktion FCOLS dargestellt. Diese verläuft durch den Punkt A, der ausgehend von FOLS die Beobachtung mit dem größten positiven Residuenwert ist und die Best-Practice-Referenz darstellt. Die Abstände der Beobachtungen zur Produktionsgrenze werden vollständig als Ineffizienzen interpretiert. Beispielsweise könnte ausgehend von Punkt B der Produktionsprozess so geändert werden, dass der Output von Beobachtung A erreicht wird. Die Strecke AB entspricht somit der Ineffizienz von B (ub COLS ). Da keine stochastischen Einflüsse berücksichtigt werden, wird die Funktion als deterministisch bezeichnet. Daraus folgt, dass bei der COLS-Methode die Ineffizienzen tendenziell überschätzt werden und sie empfindlich gegenüber Extremwerten ist. Weiter ist zu kritisieren, dass die geschätzte Produktionsgrenze immer eine Parallele der anhand der OLS Methode geschätzten Durchschnittsproduktionsfunktion ist, da diese nach oben verschoben wird. Dies impliziert jedoch, dass der Produktionsprozess von effizient produzierenden Firmen entlang der Produktionsgrenze der gleiche ist wie von allen ineffizient produzierenden Firmen unterhalb der Funktion.
Ein weiteres parametrisches Verfahren, das weniger sensitiv auf Extremwerte reagiert, ist die SFA.
(Vgl. auch den Beitrag SFA in dieser website mit einem praktischen Beispiel aus unserer Arbeit)
Auch dieses Verfahren schätzt eine Produktionsgrenze, die durch eine oder mehrere Firmen, deren Input-Output-Kombination als effizient gelten, determiniert wird. Im Unterschied zur deterministischen COLS-Methode werden die Abweichungen der beobachteten Input-Output-Kombinationen zur Produktionsgrenze jedoch nicht unbedingt vollständig als Ineffizienz interpretiert, sondern berücksichtigen auch Zufallseinflüsse, weshalb die geschätzte Funktion als stochastisch bezeichnet wird. Dies können z. B. kurzfristige Preisschocks auf Rohstoffmärkten oder unvorhersehbare Wetterbedingungen sein, die sich auf das Outputniveau auswirken.
Für die stochastische Abweichung wird angenommen, dass sie zweiseitig unbeschränkt und normalverteilt ist. In Abbildung 6 wird für die Beobachtung A ein positiver stochastischer Einfluss ( va SFA ) geschätzt, der den für den angenommenen funktionalen Zusammenhang unerwartet hohen Output im Verhältnis zu den eingesetzten Inputs erklärt. Dieser zufällige Einfluss führt dazu, dass die geschätzte Produktionsgrenze FSFA unterhalb von A liegt. Da sie dennoch unter allen Beobachtungen diejenige mit dem höchsten Outputniveau ist, wird sie als Best-Practice-Fall festgelegt und hat somit einen Ineffizienzwert ua SFA von 0. Es wird deutlich, dass der SFA-Schätzer weniger sensitiv gegenüber Extremwerten ist. Für die Beobachtung B wird ein negativer stochastischer Einfluss ( ub SFA ) geschätzt. Der Abstand zwischen der Beobachtung und der geschätzten Produktionsgrenze wird nun nicht mehr vollständig als Ineffizienz interpretiert, sondern berücksichtigt die Zufallsschwankung, sodass nur die Differenz SFA ub als Ineffizienz gewertet wird. Da für ui nur negative Abweichungen von der Produktionsgrenze möglich sind, wird für diesen Parameter eine Halb-Normalverteilung angenommen. Wie auch bei der COLS-Methode können für die Schätzung der SFA-Produktionsgrenze verschiedene funktionale Zusammenhänge angenommen werden. Diese werden in der Regel mit der Maximum Likelihood-Methode geschätzt, bei der die Koeffizienten ( β ) der Schätzgleichung so bestimmt werden, dass die Wahrscheinlichkeit, die tatsächlich beobachteten Daten zu erhalten, maximiert wird. Wie auch bei der COLS-Regression ermöglicht die SFA die Schätzung einer Produktionsgrenze, bei der mehrere Inputs und Outputs gleichzeitig berücksichtigt werden. Anstatt einer Produktionsfunktion wird in diesem Fall eine Distanzfunktion geschätzt.
Vergleich der Verfahren:
Der beschriebene Ansatz zum Effizienzvergleich anhand von preisbasierten Kennzahlen hat gegenüber anderen Methoden den Vorteil, dass er relativ leicht zu berechnen ist und schon für zwei Beobachtungen Vergleiche durchgeführt werden können. Ein wesentlicher Nachteil ist jedoch, dass sowohl Preis- als auch Mengendaten für die eingesetzten Inputs und produzierten Outputs benötigt werden, um die Indizes zu berechnen.
Bei den Verfahren, bei denen zur Effizienzmessung eine Randfunktion beziehungsweise. Produktionsgrenze bestimmt wird, reicht es, Daten über die Mengen von Inputs und Outputs zur Verfügung zu haben. Innerhalb der Gruppe der nicht-parametrischen Verfahren werden im Gegensatz zur DEA bei der FDH-Methode aufgrund der Nichtkonvexität der Randfunktion nur beobachtete und keine virtuellen Punkte berücksichtigt. Hierdurch kann die sehr restriktive Annahme unendlicher Teilbarkeit von Inputs und Outputs, wie bei der DEA, fallen gelassen werden. Allerdings erlaubt diese Vorgehensweise auch die Verwendung von Einheiten als Vergleichsmaßstab, die selbst von anderen Einheiten dominiert werden . Innerhalb der Gruppe der nicht parametrischen Verfahren weist die COLS gegenüber der SFA den Nachteil auf, dass sie deterministisch ist und somit keine stochastischen Schwankungen berücksichtigt.
Die am weitesten verbreiteten Methoden zur Effizienzmessung sind die DEA und die SFA
(Ein Vergleich zwischen SFA und DEA im Wassermanagement findet sich bei Hirschhausen, Uni Dresden)
(SFA und DEA Studie der schweizer SECO zur Effizienz der Energieversorgung in der Schweiz)
Im Folgenden werden die Vor- und Nachteile parametrischer und nicht parametrischer Verfahren anhand dieser beiden Methoden miteinander verglichen. Der große Vorteil der SFA gegenüber der DEA ist, dass sie stochastische Schwankungen berücksichtigt. Dies macht die Methode unempfindlicher gegenüber Extremwerten. Bei der DEA hingegen werden die Abstände zwischen der berechneten Randfunktion und den Beobachtungen vollständig als Ineffizienzen interpretiert, sodass diese tendenziell überschätzt werden. Somit stellt die SFA ein konservativeres Maß dar.
Ein wesentlicher Nachteil der SFA besteht jedoch in der Notwendigkeit, einen funktionalen Zusammenhang für die zu schätzende Produktionsfunktion spezifizieren zu müssen. Diese Einschränkung kann allerdings dadurch abgemildert werden, dass ein möglichst flexibler Funktionstyp, z. B. eine Translog-Funktion, gewählt wird, um den Zusammenhang zwischen Inputs und Outputs zu beschreiben. Darüber hinaus müssen bei der SFA Annahmen über die Verteilung der Komponenten des Fehlerterms ui und vi getroffen werden, um die Funktion schätzen zu können, was die Flexibilität der Methode zusätzlich einschränkt. Gleichzeitig ermöglicht dies jedoch die formal statistische Überprüfung von Hypothesen und das Ausweisen von Konfidenzintervallen. Bei der DEA hingegen, deren Randfunktion linear programmiert wird, muss kein Funktionsverlauf vorgegeben werden, sodass das Risiko eines falsch spezifizierten Modells reduziert wird.
Eine DIW Studie untersucht mithilfe der SFA und der DEA die Effizienz vom Stromnetzen unter technischen, regionalen und unter verschiedenen Annahmen der Größe der agierenden Unternehmen. (Download dieser DIW Studie)
Eine Weiterentwicklung beider Methoden, bei denen die Vorteile miteinander verbunden werden, sind die semi-parametrischen Methoden stochastische DEA beziehungsweise. stochastische FDH. Darüber hinaus gibt es parametrische Verfahren, bei denen die funktionalen Annahmen über die Komponenten des Fehlerterms ui und vi gelockert werden. Die Gemeinsamkeiten und wesentlichen Unterschiede beider Methoden sind in Tabelle 1 zusammengefasst dargestellt
| Aspekt | DEA | SFA |
| Anzahl Inputs/Outputs | Mehrere Inputs/Outputs | Mehrere Inputs/Outputs |
| Bestimmung der Funktion | Lineare Programmierung | Ökonometrische Schätzung |
| Berücksichtigung stochastischer Schwankungen | Nein (deterministisch) | Ja (stochastisch) |
| Funktionale Spezifizierung notwendig | Nein (nicht parametrisch) | Ja (parametrisch) |
| Zerlegung der Veränderung der TFP in einzelne Komponenten möglich | Ja | Ja |
| Benötigte Daten | Mengen der Inputs und Outputs | Mengen der Inputs und Outputs |
Tab.1: Vergleich der DEA und der SFA
Insgesamt kann festgestellt werden, dass die Wahl zwischen DEA und SFA als adäquate Methode zur Effizienzmessung immer mit einem Tradeoff verbunden ist. Dabei hängt die Entscheidung unter anderem von der konkreten Fragestellung, den zur Verfügung stehenden Daten und dem gegebenen Produktionsprozess ab.
Effizienzvergleiche anhand von Preisindizes sind relativ einfach durchzuführen, lassen jedoch keine genauere Analyse der einzelnen Produktivitätstreiber zu. Die nicht parametrischen Verfahren zeichnen sich durch ihre große Flexibilität aus, da kein funktionaler Zusammenhang für die Produktion angenommen werden muss. Allerdings erlauben diese Verfahren in ihrer klassischen Form keine statistischen Rückschlüssen und keine Berücksichtigung von Zufallseinflüssen.
Im Gegensatz dazu bedarf es bei den parametrischen Verfahren a priori einer einschränkenden funktionalen Spezifizierung. Dies ermöglicht es, die Ergebnisse formal statistisch zu überprüfen und stochastische Einflüsse zu berücksichtigen. Bei den vorgestellten Methoden wurden alle Abweichungen von der bestimmten Randfunktion einem ineffizienten Produktionsprozess und bei stochastischen Modellen teilweise Zufallseinflüssen zugeschrieben. Dies impliziert jedoch, dass alle für die Effizienzbestimmung relevanten Eigenschaften der Untersuchungseinheiten beobachtet und im Modell berücksichtigt werden können.
In neueren Modellen, die für Paneldaten anwendbar sind, wird davon ausgegangen, dass Abweichungen zudem durch unbeobachtete Eigenschaften, so genannte unbeobachtete Heterogenität, der Untersuchungseinheiten zustande kommen können. Hierbei besteht jedoch die Gefahr, dass eine über die Zeit konstant ineffiziente Produktion nicht mehr als solche erkannt wird. Die Ineffizienz dieser Modelle wird somit tendenziell unterschätzt. Im Gegensatz dazu überschätzen Modelle, die keine unbeobachtbare Heterogenität berücksichtigen, die Ineffizienz, weil hierdurch verursachte Abweichungen von der Randfunktion als Ineffizienz aufgefasst werden. Da beide Modelltypen Verzerrungen hinsichtlich der tatsächlichen Ineffizienz aufweisen, können die Ergebnisse als Unter- beziehungsweise Obergrenze genutzt werden, um ein Ineffizienzintervall zu bilden. Solche Intervalle geben Aufschluss über das Potenzial von Unternehmen, die Effizienz im Produktionsprozess zu steigern, während der Einfluss von Messfehlern reduziert wird. Zusammenfassend kann fest gehalten werden, dass die Effizienzmessmethoden hinsichtlich der betriebswirtschaftlichen und volkswirtschaftlichen Fragestellungen valide Ergebnisse liefern können.
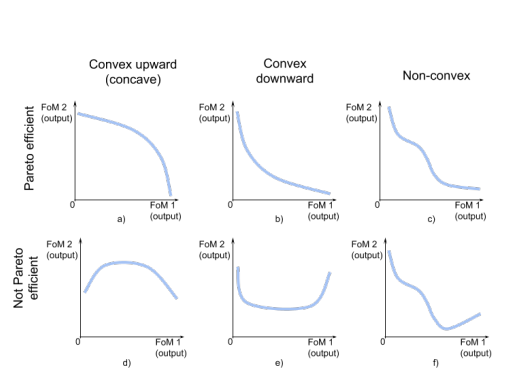
Abb.: All possible in a two-dimensional space classes ofefficient frontier shapes (only upper left is DEA compatible).
Quelle: Yuskevich, Ilya and Vingerhoeds, Rob A. and Golkar, Alessandro Comparative analysis of two-dimensional datadriven efficient frontier estimation algorithms.
(2018) In: 2018 IEEE International Systems Engineering Symposium (ISSE), 1 October 2018 - 3 October 2018 (Italy).
Ein integrierendes Konzept für diese Ansätze ist eine effiziente Grenze, die als Fläche in der n-dimensionalen definiert werden kann FoMs Raum, der alle effizienten Punkte enthält, die wir möglicherweise erreichen könnte. Eine effiziente Grenze wird als Pareto bezeichnet Grenze, wenn für jeden Punkt an der Grenze es unmöglich ist Verbesserung einer Leistungszahl (FoMs) ohne Verschlechterung der andere FoMs.
DEA-Standardmodelle (Charnes, Cooper und Rhodes (CCR)) und Banker, Charnes und Cooper (BCC) [5]) sind in der Lage um nur konvexe nach oben gerichtete paretoeffiziente Grenzen zu schätzen. Es reicht aus, um die Grenzen der Produktionsmöglichkeiten abzuschätzen Welches sind die Kompromisse bei der Herstellung der Kombination von konkurrierende Waren mit den begrenzten Ressourcen. Die Kurven, die mögliche Kompromisse zwischen den Auftritten darstellen
eines technischen Systems liegen in einem breiteren Formenspektrum vor die oft nichtlineare physikalische Natur der zugrunde liegenden Prozesse. Zum Beispiel in Abb. 1a ist konvex nach unten dargestellt Pareto effiziente Grenze, die in der Analyse zu finden ist Benzinmotor Leistung vs Meilen pro Gallone Kraftstoffverbrauch Maßnahme. U-förmige Grenzen (obige Abb. d, e) sind für Flugzeugtreibstoff üblich Effizienzanalysen. Wenn FoM 1 eine Flugzeuggeschwindigkeit ist, dann ist die
Total Airdrag (FoM 2) hat eine U-Form als Verbindung mit zunehmender Geschwindigkeit parasitärer Widerstand und abnehmender mit Geschwindigkeitslift-induzierter Widerstand. Der einfachste Weg, eine Grenze mit Konkavitätskonvexitätsänderungen (nicht konvex) zu erhalten, ist die Analyse des zusammengesetzten FoM von der Grenze der U-Form und konvex nach unten Pareto effizient Grenze (obige Abb. c).
In der Praxis passiert dies, wenn wir versuchen zu schätzen Ein breites Technologiefeld mit komplexer Physik dahinter. Als Beispiel hängt der Wirkungsgrad der Leistungsumwandlung ab Wellenlänge in Solarzellen zeigen ein solches Verhalten.
Lassen Sie uns nun zeigen, dass U-förmige Grenzen nicht paretoeffizient sind.
Angenommen, wir möchten im Idealfall beide FoMs maximieren. Niedrige Werte der FoM 1-Grenze verhalten sich wie gewohnt paretoeffizient Grenze. Für FoM 1 hohe Werte beobachten wir gleichzeitig Verbesserung beider FoMs (was im Widerspruch zur Definition der Pareto-Effizienz steht). Das heißt nicht, dass optimal Lösungen für alle Anwendungen gibt es nur in diesem Teil von Grenze. Angenommen, FoM 1 in unserem Beispiel ist die Kapazität von ein Transportsystem. Im Allgemeinen möchten wir maximieren Kapazität. Kapazität ist jedoch oft mit Größe verbunden, Dies kann für einige Anwendungen eingeschränkt sein. In Technologieplanungsprozessen ist es jedoch oft sinnvoll, alle Optionen unabhängig von der Anwendung zu erkunden, um dies zu sehen ganzes Bild. Es ist daher wichtig, eine gute Schätzung zu erhalten Grenzen jeglicher Form, um zu wissen, was technisch erreichbar ist. Das Hauptziel von Grenzschätzungsalgorithmen besteht darin,
konstruieren die Grenze genau und effizient. Die mathematische Einstellung für modellbasierte und datengesteuerte Fälle ist jedoch komplett anders. Für die modellbasierte Schätzung haben wir ein Modell, das es uns erlaubt um so viele Punkte wie nötig zu generieren. Wenn die Grenze a ist kontinuierliche Funktion dann die Anzahl der Punkte, die sein könnten theoretisch unbegrenzt generiert. Wenn die Einstellung diskret ist wir kann theoretisch eine volle Grenze als die Anzahl von konstruieren mögliche Werte sind begrenzt. Bei der datengetriebenen Schätzung haben wir die Punkte bereits in Form von Marktdaten und der Anzahl generiert Die Anzahl der Punkte ist daher immer begrenzt. In diesem Fall können wir nie
eine perfekte Information über die Grenze erreichen. Bei der modellbasierten Schätzung wird die Berechnung von FoMs für Jeder Entwurfspunkt kann eine erhebliche Zeitdauer in Anspruch nehmen (z. B. um die Verstärkung der Mikrowellenantenne mit spezifisch zu berechnen Konfiguration muss man möglicherweise eine Reihe von elektrodynamischen lösen Differentialgleichungen mit FEM). Deshalb viele Anstrengungen in Dieses Gebiet widmete sich der Entwicklung von speziellen Methoden, deren Ziel es ist, Lösungen zu generieren, die gleichmäßig verteilt sind der Designraum mit dem Ziel, den Rechenaufwand zu reduzieren Zeit, um das Problem der multiobjektiven Optimierung zu lösen [7] - [9].inige Methoden geben als wichtiges Unterziel das an Fähigkeit, die Grenzkonkavitäts-Konvexitäts-Änderungen zu überwinden.
Die Klassifizierung entsprechender Algorithmen zur Schätzung der Effizienzgrenzen zeigt untenstehende Abb.
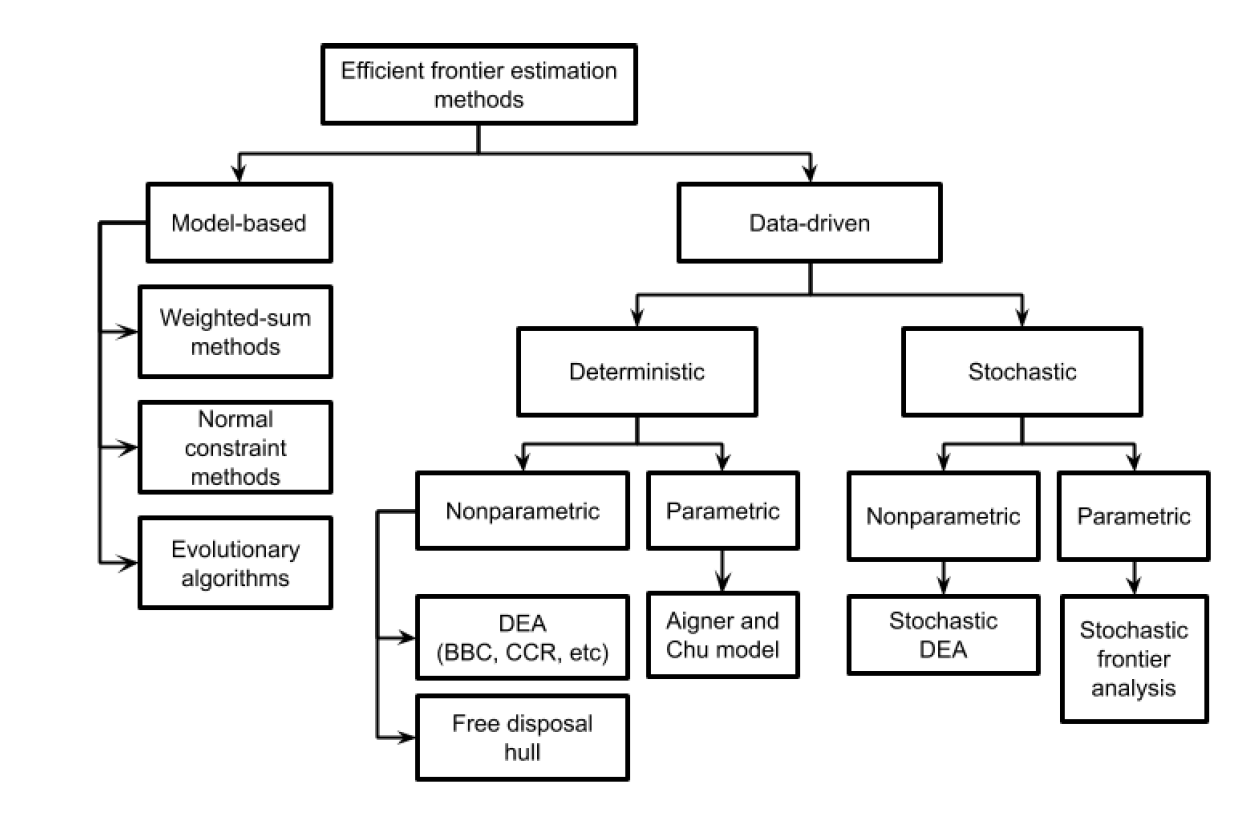
Abb.:Efficient frontier estimation algorithms classification
Quelle: Yuskevich, Ilya and Vingerhoeds, Rob A. and Golkar, Alessandro Comparative analysis of two-dimensional datadriven efficient frontier estimation algorithms.
(2018) In: 2018 IEEE International Systems Engineering Symposium (ISSE), 1 October 2018 - 3 October 2018 (Italy).